Solving an equation implicitly

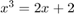Solving for $x$ satisfying $x^3 = 2x+2$.

Contents

Define each side of the equation

clear all

f = @(x) x^3;
g = @(x) 2*x + 2;

Write objective function

Solving 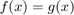$f(x)=g(x)$ is equivalent to solving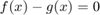 $f(x)-g(x)=0$

objfn = @(x) f(x) - g(x);

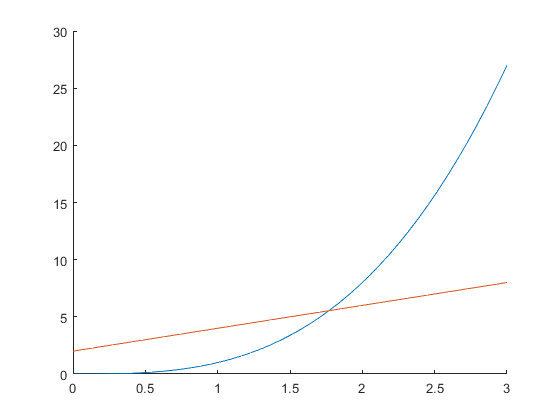
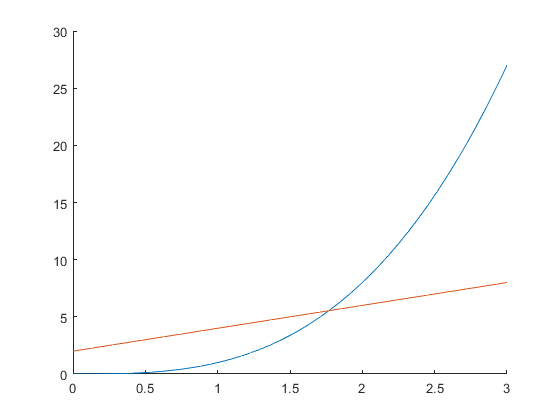
Try to determine a rough guess for the solution

Solution might not be unique! Graphing can help determine uniqueness as well as initial guess, but not so much if you have many dimensions. Might have to try different initial guesses. Theory can often help give reasonable guess or otherwise restrict the domain (e.g. only non-negatives).

hold on
    fplot(@(x) f(x), [0 3])
    fplot(@(x) g(x), [0 3])
hold off

% Looks like about 1.8 or so is a good guess.

Warning: Function behaves unexpectedly on array inputs. To improve performance,
properly vectorize your function to return an output with the same size and
shape as the input arguments.

Solve for root of objective function

The second argument of fsolve is the guess for $x$.

fsolve(objfn,1.8)

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.


ans =

    1.7693


Published with MATLAB® R2019a